drawing 3d regions of integration

Although nosotros define triple integrals using a Riemann sum, we normally evaluate triple integrals by turning them into iterated integrals involving three single integrals. I tricky part of triple integrals is describing the three-dimensional regions of integration and the resulting premises on the iterated integrals. Forming double iterated integrals is easier because one can describe the domain and label all the edges and corners, which makes determining the bounds more tractable. 3-dimensional regions are much more hard to visualize or draw, which can make the prospect of determining integration bounds a formidable task.

Fortunately, there are means to reduce a triple integral into a double integral combined with a unmarried integral. One such method is i we telephone call the "shadow method," which we describe here. A related method is i we telephone call the "cantankerous department method" which we describe on some other page.

In the shadow method, you lot imagine there is a light source, such as the sun, positioned far abroad along i of the coordinate axis (such as the positive $z$-centrality). Nosotros'll retrieve of this sun as being straight up in the sky and think of the chosen coordinate axis every bit though information technology were vertical.

As this sun is shining on the three-dimesional region $\dlv$ of our integral, information technology is casting a shadow onto the apartment ground below the region, i.e., on a plane perpendicular to the axis the sunday is coming from. This shadow is a two-dimensional region, and we turn the triple integral over $\dlv$ into a double integral over the shadow. Inside the double integral, we still need to include a single integral in the third "vertical" variable, where this variable ranges from the bottom of $\dlv$ to its top. If, for example, we had called $z$ to be the "vertical" variable where the lord's day is coming from, the shadow method for integrating a function $f$ over $\dlv$ would be of the form \brainstorm{get together*} \iiint_{\dlv}f(10,y,z)dV = \iint_{\text{shadow}} \left( \int_{\text{lesser}(x,y)}^{\text{meridian}(10,y)} f(x,y,z) dz\right) dx\,dy. \terminate{gather*} But, we don't demand to take the sun coming from the $z$ direction. It might be easier to let the sun be in the $x$ direction, giving an integral of the form \begin{gather*} \iiint_{\dlv}f(10,y,z) dV= \iint_{\text{shadow}} \left( \int_{\text{bottom}(y,z)}^{\text{top}(y,z)} f(x,y,z) dx\right) dy\,dz, \end{assemble*} or let the sun beingness in the $y$ direction, giving an integral of the form \begin{gather*} \iiint_{\dlv}f(x,y,z)dV = \iint_{\text{shadow}} \left( \int_{\text{lesser}(x,z)}^{\text{top}(ten,z)} f(x,y,z) dy\right) dx\,dz. \stop{assemble*} We tin choose the centrality we use for the "vertical" direction based on the shape of the region $\dlv$.

The use of the shadow method is best illustrated by examples.

Example one

Let $\dlv$ be the iii-dimesional region divisional by the vertical planes $x=0$, $y=one$, and $10=y$ likewise as the angled planes $z=two+10-y$ and $z=x-y$. Let $f(x,y,z)=xy$ and compute the integral of $f$ over $\dlv$.

Solution: Given that there are 3 planes parallel to the $z$-centrality, nosotros'll use the $z$ direction as the vertical direction. Nosotros'll retrieve of the sun every bit coming from that direction and casting a shadow beneath it. As shown by the below figure, those iii vertical planes cause $\dlv$ to bandage a triangular shadow.

Applet loading

Region divisional by planes demonstrating the shadow method. The region $\dlv$ is divisional past the vertical planes $x=0$, $y=1$, and $ten=y$ and the angled planes $z=2+x-y$ and $z=x-y$. If the sun is viewed to exist in the management of the positive $z$-axis, the resulting shadow on a plane perpendicular to the $z$-centrality is a triangle, equally illustrated by the bluish triangle below the region.

More information virtually applet.

Co-ordinate to the shadow method, we demand to integrate $x$ and $y$ over this shadow. Then, for each signal $(x,y)$ in the shadow, we need to integrate $z$ from the bottom to the top of $\dlv$. The bottom and top are formed by the angled planes, so the range of $z$ for each point in the shadow is \begin{get together*} x-y \lt z \lt 2+10-y. \cease{get together*} The inner integral is therefore \begin{gather*} \int_{\text{bottom}(ten,y)}^{\text{top}(10,y)} f(10,y,z) dz = \int_{ten-y}^{ii+10-y}f(x,y,z)dz. \terminate{get together*}

The outer double integral is an integral over the shadow. The shadow is the maximal extend of $\dlv$ in the $x$ and $y$ directions. For this example, the shadow is fairly uncomplicated, since the extent of $\dlv$ is adamant by the 3 vertical planes $x=0$, $y=i$ and $10=y$. In whatsoever plane parallel to the $xy$-plane, these planes become lines given by the same equations (as the original equations don't contain a $z$). The shadow is the triangle bounded by the lines $x=0$, $y=1$ and $10=y$.

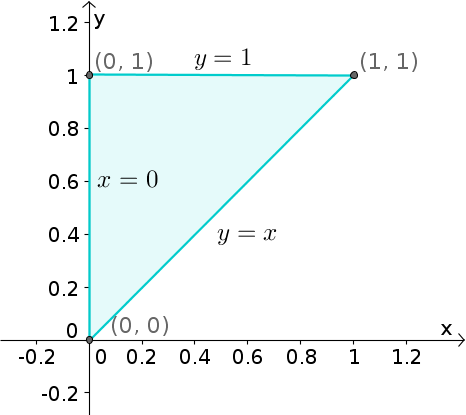
To find premises for the double integral over the shadow, nosotros'll permit $10$ exist the inner integral. For any value of $y$, $x$ ranges from $x=0$ to $x=y$ so the range of $x$ is \begin{assemble*} 0 \lt x \lt y. \end{gather*} The maximum range of $y$ is shadow is \brainstorm{get together*} 0 \lt y \lt ane. \terminate{get together*} Therefore, the double integral over the shadow is of the form \begin{gather*} \iint_{\text{shadow}} \cdots dx\,dy = \int_0^i \int_0^y \cdots dx\,dy. \end{gather*}

Putting all the limits of integration together and inserting the integrand $f(10,y,z)=xy$, we calculate the integral: \begin{align*} \iiint_{\dlv}f(x,y,z)dV &=\int_0^1 \int_0^y \int_{10-y}^{two+10-y} xy\, dz\,dx\,dy\\ &= \int_0^1 \int_0^y xyz \bigg|_{z=x-y}^{z=2+x-y} dx\,dy\\ &= \int_0^1 \int_0^y 2xy dx\,dy\\ &= \int_0^one x^2y \bigg|_{10=0}^{x=y}dy\\ &= \int_0^1 y^iii dy = \frac{y^4}{4}\bigg|_0^1 = \frac{1}{4}. \terminate{marshal*}

Example ii

Allow $\rho(x,y,z)$ be the charge density at the bespeak $(10,y,z)$ inside an object $\dlv$ bounded by the elliptic paraboloids $y=5-4 ten^two-z^two$ and $y=x^ii+z^ii/iv$. Gear up the integral giving the total charge inside $\dlv$.

Solution: The total charge is the integral of the charge density $\rho$ over the region $\dlv$: \begin{gather*} \text{total accuse} = \iiint_{\dlv} \rho(ten,y,z) \, dV. \end{gather*} Our chore is to calculate the limits of integration determined by $\dlv$.

For this region, the shadow method will work well if nosotros choose the $y$-centrality as the "vertical" direction, i.due east., the management where the sun comes from. If the positive $y$ direction is up, then ane boundary, $y=5-4 10^2-z^ii$, is a paraboloid opening down that intersects the $y$-centrality at $y=five$. The other boundary, $y=x^2+z^2/4$ is a paraboloid that opens upwards and intersects the $y$-axis at the origin. Therefore, the bounded region $\dlv$ between the surfaces will be the region below $y=5-4 ten^2-z^two$ and above $y=10^two+z^2/4$, i.e., the region described by $$10^ii+\frac{z^two}{4} \le y \le 5-4 x^two-z^two,$$ as illustrated below. The two paraboloid surfaces are the summit and bottom limits for the shadow method, \begin{gather*} \int_{\text{bottom}(x,z)}^{\text{acme}(x,z)} \rho(x,y,z) dy = \int_{x^two+z^2/four}^{5-4 x^2-z^2}\rho(x,y,z)dy. \end{gather*}

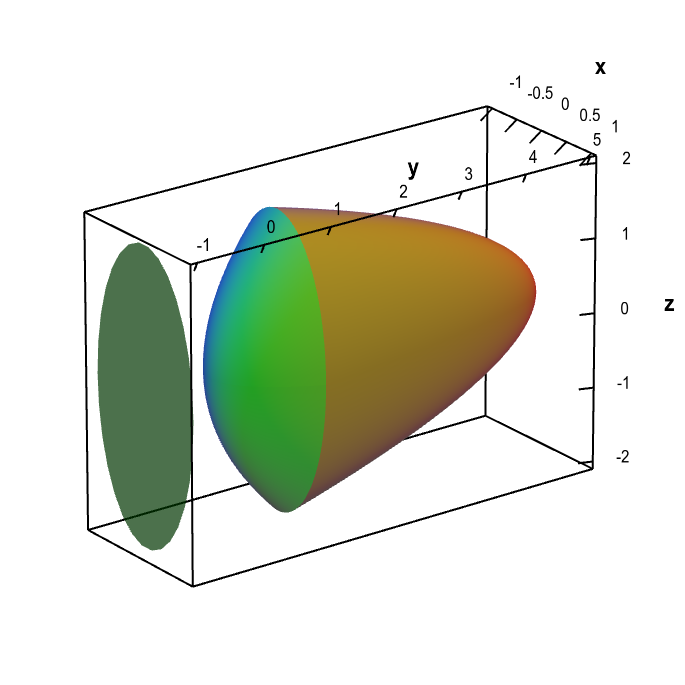
Applet loading

Region bounded by paraboloids demonstrating the shadow method. The region $\dlv$ is bounded by the elliptic paraboloids $y=5-4 10^2-z^ii$ and $y=ten^2+z^ii/4$. If the sunday is viewed to exist in the direction of the positive $y$-centrality, the shadow of $\dlv$ in a plane perpendicular to the $y$-axis is the region inside the ellipse $10^2+z^2/4=i$.

More information about applet.

The remaining task is to decide the shadow of $\dlv$, illustrated by the ellipse, above. The widest part of $\dlv$ is where the ii paraboloids intersect, i.e., where $$10^2+\frac{z^2}{4} = five-4 ten^2-z^2,$$ which can exist written more just as $$ten^2+\frac{z^ii}{4} = ane.$$ This purlieus of the shadow is an ellipse with a semi-major axis of ii and a semi-minor axis of one. The shadow itself is the region $$10^two+\frac{z^2}{4} \le ane,$$ which includes the interior of the ellipse, shown below.

Since within the ellipse, $ten^2 \le one- z^2/4$, the range of $10$ for each value of $z$ is $$ -\sqrt{one-z^2/4} \le x \le \sqrt{i-z^two/4}.$$ The maximum range of $z$ is $-2 \le z \le 2$, so the integration limits for the shadow are \begin{assemble*} \iint_{\text{shadow}} \cdots dx\,dz = \int_{-two}^two \int_{-\sqrt{1-z^two/4}}^{\sqrt{ane-z^2/4}} \cdots dx\,dz. \terminate{get together*}

Putting the top and bottom limits together with the shadow, we conclude that the full charge within $\dlv$ is the integral \begin{marshal*} \text{full charge} &= \iiint_{\dlv} \rho(x,y,z) \, dV\\ &=\int_{-ii}^two \int_{-\sqrt{ane-z^two/four}}^{\sqrt{i-z^ii/4}}\int_{x^2+z^2/4}^{5-four x^two-z^2}\rho(10,y,z)dy\,dx\,dz. \terminate{align*}

payneounkentoot1954.blogspot.com

Source: https://mathinsight.org/triple_integral_shadow_method